O que é Modelagem Estatística
Vivemos em uma era em que dados são coletados o tempo todo, em praticamente todas as áreas do conhecimento e setores da sociedade. No contexto da Estatística, um dos principais objetivos da Modelagem Estatística é estudar a relação entre variáveis por meio da construção de modelos matemáticos que descrevem e explicam padrões nos dados.
Nesse processo, determinamos uma ou mais variáveis resposta (ou dependentes), cujo comportamento buscamos compreender, e as relacionamos a covariáveis (ou variáveis explicativas), que podem influenciar esses resultados. Por exemplo, podemos modelar a relação entre a altura e o peso de uma pessoa ou analisar fatores que afetam as vendas de um produto em uma empresa.
No ambiente corporativo, na pesquisa científica e até em decisões cotidianas, compreender essas relações é essencial para a tomada de decisões baseada em dados. Um modelo bem construído pode ajudar a prever cenários, otimizar recursos e fornecer insights valiosos para diferentes áreas, como saúde, economia, marketing e engenharia.
Para tornar esse conceito mais concreto, veremos dois exemplos práticos que demonstram como a modelagem estatística pode ser uma ferramenta poderosa na análise de dados. No entanto, vale destacar que o foco aqui será na construção do modelo e na interpretação de seus resultados, assumindo que etapas fundamentais, como Análise Exploratória e Validação do Modelo, já foram devidamente conduzidas, ainda que não sejam apresentadas neste momento.
Exemplo 1 – Fatores que Influenciam o Desempenho de Funcionários
Neste primeiro exemplo, analisamos uma livraria física com 100 funcionários, que têm a função de conversar com clientes para recomendar e vender livros. O objetivo do estudo é entender quais características dos funcionários influenciam suas vendas. Para isso, todos trabalharam sob as mesmas condições e horários, e foi registrada a média diária de faturamento de cada um.
Além disso, a empresa considera investir em um curso de vendas para aprimorar as habilidades dos funcionários, mas antes quer avaliar se esse investimento realmente traz retorno. Para isso, 15 vendedores foram selecionados aleatoriamente para participar do curso, permitindo uma comparação entre aqueles que fizeram e os que não fizeram o treinamento.
Sendo assim, nossa variável resposta é o faturamento médio diário de cada funcionário e temos como covariáveis a serem utilizadas: Idade, Número Médio de Livros Lidos por Mês, Escolaridade (Ensino Médio/Graduação), Experiência Prévia ao Experimento (em dias trabalhados), Participação em um Clube do Livro (Participa/Não Participa), Fluência em Inglês (Fluente/Não Fluente) e Participação no Curso de Vendas (Participou/Não Participou). Para analisar esses dados, utilizamos um modelo de Regressão Linear Simples, que expressa o faturamento médio diário como uma combinação ponderada das demais variáveis. Em outras palavras, cada variável recebe um coeficiente que indica o impacto que ela tem sobre as vendas.
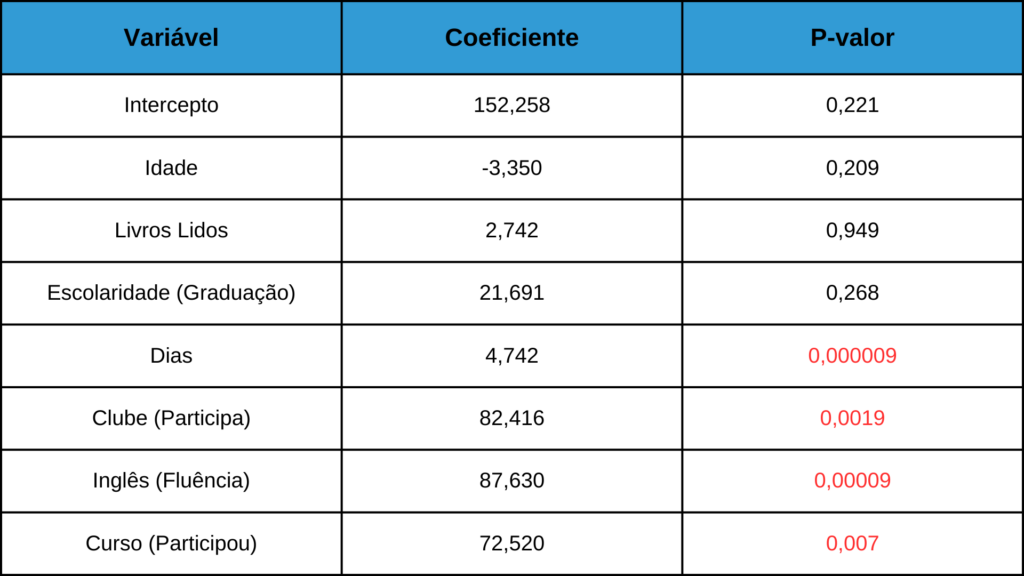
Na primeira coluna da tabela, estão listadas as variáveis analisadas. A segunda coluna mostra os coeficientes da regressão, que indicam a relação de cada variável com o faturamento médio mensal. Já a terceira coluna apresenta o p-valor, que nos ajuda a determinar se a influência de cada variável é estatisticamente significativa.
Para tomar essa decisão, usamos um ponto de corte de 0,05, correspondente a um nível de confiança de 95%. Se o p-valor de uma variável for maior que 0,05, concluímos que ela não tem um efeito significativo sobre o faturamento médio mensal. No nosso exemplo, Idade, Número de Livros Lidos por Mês e Escolaridade não demonstraram uma relação estatisticamente relevante com o faturamento.
Por outro lado, Experiência Prévia, Participação em Clube do Livro, Conhecimento de Inglês e Participação no Curso de Vendas foram identificadas como variáveis significativas (intercepto é um coeficiente sem interpretação prática nesse cenário, e está presente por fins matemáticos). Isso significa que elas têm um impacto relevante no faturamento médio mensal.
A interpretação dos coeficientes funciona da seguinte maneira:
- Para variáveis numéricas, o coeficiente indica quanto, em média, o faturamento aumenta para cada unidade adicional da variável. Por exemplo, cada dia adicional de Experiência Prévia está associado a um aumento médio de R$ 4742 no faturamento mensal.
- Para variáveis categóricas (como participação ou não em um curso), o coeficiente representa a diferença média entre os grupos. Por exemplo, funcionários que participaram do Curso de Vendas faturam, em média, R$ 72 a mais por dia do que aqueles que não participaram.
Com essa análise, nós conseguimos identificar quais fatores realmente influenciam o faturamento, ajudando na tomada de decisões estratégicas com base em dados. Ademais, foi avaliado se o curso de fato foi impactante, e obtivemos um aumento médio de 72 reais no faturamento, então é possível utilizar esse resultado para decidir contratar ou não esse curso para outros funcionários.
Exemplo 2 – Atributos Relacionados a uma Pessoa Comprar em um Site
Neste segundo exemplo, temos uma empresa que vende seus produtos de forma remota por meio de um site e, em determinado dia, optou por coletar os dados de todos que acessam o site, independente se finalizaram a compra ou não a fim de determinar quais fatores podem estar relacionados a uma pessoa efetivamente se tornar um cliente tendo acessado a loja.
Sendo assim, a nossa variável resposta é um indicador se a pessoa finalizou a compra ou não e temos como variáveis a serem utilizadas: Tempo de Permanência no Site (em minutos), Gênero, Idade, Origem do Tráfego (Orgânico/Pago), Dispositivo de Acesso (Celular/Computador), Período do Acesso (Dia/Noite) e Valor Total no Carrinho (em reais). Para analisar esses dados, utilizamos a Regressão Logística, que expressa o logaritmo natural das odds do evento como uma combinação ponderada das demais variáveis. Ajustando um modelo com todas as variáveis, os resultados obtidos estão presentes na tabela abaixo:
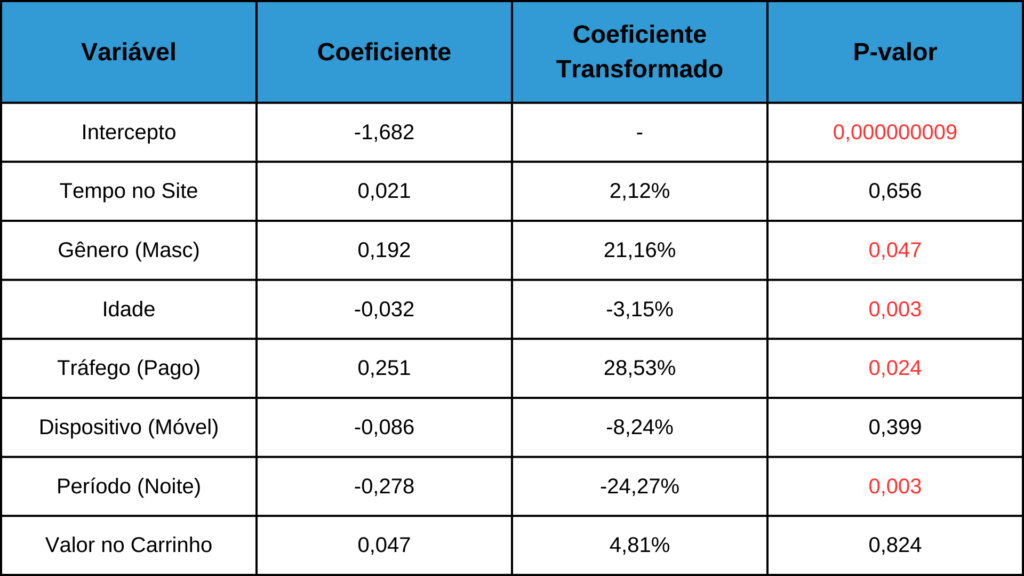
Na primeira coluna da tabela, estão listadas as variáveis analisadas. Já na segunda coluna, estão apresentados os coeficientes, que não possuem uma interpretação tão direta quanto no caso anterior. Para resolver esse problema, a terceira coluna apresenta uma transformação dos coeficientes (com exceção do intercepto), assim temos uma visão de como está sendo a influência. A quarta coluna possui os p-valores, que possuem a mesma interpretação que no caso anterior.
Nesse caso, as variáveis não significativas foram Tempo no Site, Dispositivo de Acesso e Valor Total no Carrinho. Por outro lado, Gênero, Idade, Tráfego e Período do Acesso representaram um impacto significativo para representar a probabilidade de determinado acesso ao site resultar em uma compra (assim como no caso anterior, o intercepto não possui uma interpretação direta, estando presente apenas por fins matemáticos).
Como a nossa variável de interesse é categórica, estamos interessados na probabilidade dela assumir determinado valor, no caso, a de compra. Para isso, definimos as odds, que são a divisão entre a probabilidade de ocorrer e a de não ocorrer (Por exemplo, para odds igual a 2, a chance de ocorrer é 2 vezes maior que a de não ocorrer). A interpretação dos coeficientes transformados é dada por:
- Para variáveis numéricas, o coeficiente transformado (que é uma porcentagem) indica quanto, em média, as odds aumentam para cada unidade adicional da respectiva variável. Por exemplo, a cada aumento de um ano na idade de uma pessoa, as odds reduzem em média 3,15%.
- Para variáveis categóricas (como participação ou não em um curso), o coeficiente transformado representa a diferença média entre os grupos. Por exemplo, para pessoas que chegam por tráfego pago, as odds aumentam em média 28,53%.
Com essa análise, conseguimos analisar os fatores que influenciam em uma pessoa comprar ou não no site. Além de ter uma percepção melhor sobre o público alvo e alguns hábitos, também foi possível quantificar o real impacto médio do tráfego pago.
Conclusão
Portanto, vimos que a Modelagem Estatística é uma ferramenta muito poderosa para aprimorar os resultados de empresas ao conhecer de maneira profunda a relação entre diversas variáveis em conjunto. A partir de um modelo estatístico, as tomadas de decisão são muito mais embasadas, pois conhecer de verdade como os dados se comportam é uma ferramenta para o sucesso.
Acredita que essas análises ajudarão sua empresa? Entre em contato com a Estat Júnior, estamos prontos para propor e realizar modelos que impactarão seus resultados.


1 comentário em “Alavancando os Resultados de sua Empresa com Modelagem Estatística”
Ótimo texto!