No dia a dia, diversos fenômenos ocorrem a todo momento, e identificar padrões nesses eventos é de extremo interesse. Um dos principais objetivos da Estatística é justamente estudar características associadas a eventos que, à primeira vista, parecem imprevisíveis.
Foi observado que, em muitas situações reais, existe um padrão na probabilidade do primeiro dígito de um determinado número. Essa ideia foi desenvolvida e resultou na Lei de Benford, cuja forma mais simples expressa a probabilidade do primeiro dígito por meio de uma fórmula logarítmica. Atualmente, essa noção tem diversas aplicações, sendo uma das principais a detecção de fraudes em conjuntos de dados quando o padrão não é seguido.
História
No fim do século XIX, o astrônomo Simon Newcomb foi o primeiro a observar esse fenômeno de forma bem inusitada. Na época, como não existiam calculadoras, eram utilizados livros que catalogavam diversos resultados de logaritmos para facilitar os cálculos. Newcomb notou que as páginas dos logaritmos iniciados por algarismos menores estavam mais desgastadas que as demais. A partir disso, estudou o padrão e propôs um modelo para a probabilidade do primeiro dígito.
No século XX, Frank Benford retomou o estudo desse fenômeno e trabalhou para sua ampla divulgação. Ele generalizou o modelo e analisou bases de dados das mais diversas áreas para verificar a validade do padrão. Em 1938, publicou o artigo “The Law of Anomalous Numbers”, em que testou a Lei de Benford em mais de 20 mil números provenientes de diferentes contextos, como comprimento de rios, tamanho de populações, taxas de mortalidade, constantes físicas e massas atômicas.
Atualmente, como o padrão foi identificado em diversos cenários, ele é utilizado para detectar fraudes. De maneira intuitiva, muitas pessoas esperam que os dígitos dos números sejam distribuídos de forma uniforme, isto é, todos com igual proporção. Dessa forma, ao falsificar dados, é comum que os algarismos estejam de maneira equilibrada, fugindo do padrão esperado pela Lei de Benford.
Por exemplo, em 1999, Mark Negrini publicou “I’ve got your number”, demonstrando como a Lei de Benford pode ser utilizada para detectar fraudes contábeis. Em 2007, Andreas Diekmann publicou “Not the first digit!”, abordando sua aplicação na detecção de fraudes científicas utilizando coeficientes de Regressão Linear.
Explicação da Lei de Benford
Após apresentar o contexto histórico, resta analisar como essas probabilidades se manifestam na prática. O modelo estabelece que, em situações onde a Lei de Benford é válida, a probabilidade de um número ter um determinado primeiro dígito d (variando de 1 a 9) é dada por:
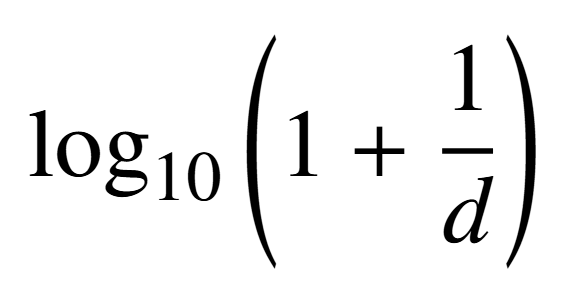
Para uma melhor visualização, a probabilidade de cada algarismo ser o primeiro dígito de um número de acordo com a Lei de Benford está presente no gráfico abaixo:
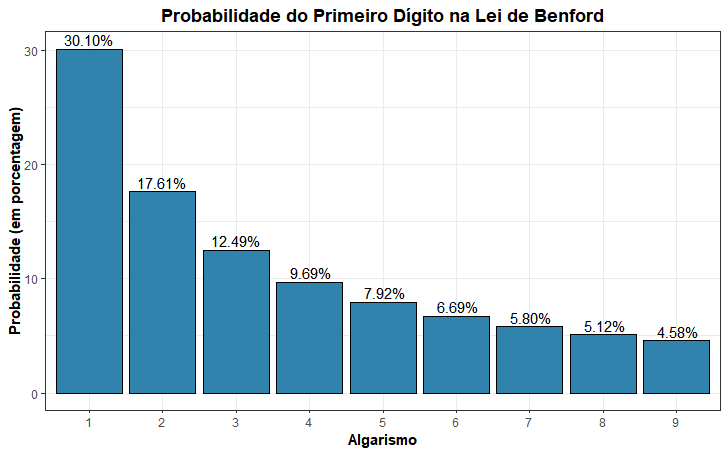
Além de considerar apenas o primeiro dígito, é possível generalizar a Lei de Benford para sequências de algarismos ou dígitos específicos. No entanto, quanto maior a posição do dígito analisado, mais a distribuição tende à uniformidade, ou seja, todos os algarismos passam a ter chances iguais de ocorrer.
Exemplos
A fim de ilustrar aplicações da Lei de Benford, serão utilizados 3 exemplos:
- Sequência de Fibonacci: série matemática onde cada termo é a soma dos dois anteriores, começando com 0 e 1. Os primeiros termos são: 0, 1, 1, 2, 3, 5, 8, 13, 21…
- PIB: conjunto de dados contendo o PIB (Produto Interno Bruto) de todos os países em 2022.
- População: conjunto de dados contendo o número total de habitantes de todas as cidades brasileiras em 2024.
O gráfico abaixo mostra as proporções dos primeiros dígitos nos dados analisados (barras) e os valores esperados segundo a Lei de Benford (linha).
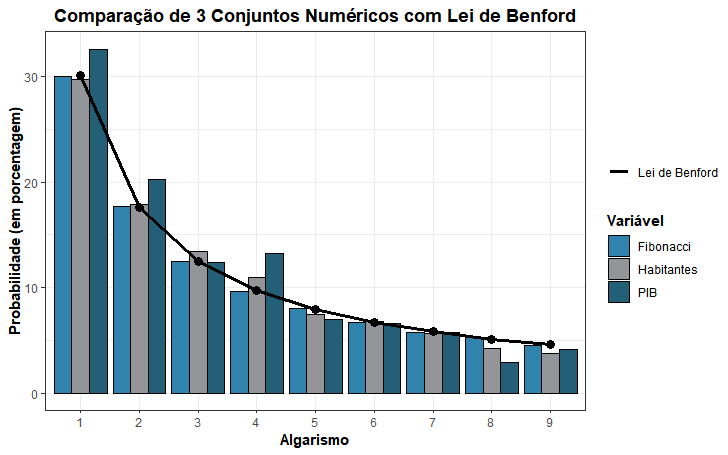
Os resultados mostram que a proporção observada nos três conjuntos de dados se aproxima muito do padrão esperado pela Lei de Benford. Assim, essa lei se revela uma ferramenta poderosa para identificar padrões naturais nos dados e detectar inconsistências, sendo utilizada na análise de fraudes e anomalias estatísticas.

