Introdução
Ao realizar pesquisas científicas, um procedimento recorrente é a análise de dados coletados a partir de uma amostra, com o objetivo de generalizar os resultados obtidos para toda a população de interesse. Entretanto, simplesmente apresentar gráficos e tabelas não é suficiente para responder de forma contundente às questões de pesquisa, uma vez que pode haver certa subjetividade na interpretação dos dados.
Por exemplo, se o objetivo é comparar a média de altura de dois grupos e a diferença observada foi de 5 cm, como saber se esses 5 cm são realmente significativos? E se a diferença fosse de apenas 2 cm? Os resultados mudariam?
Para resolver esse tipo de dúvida e proporcionar maior confiabilidade aos resultados, existem ferramentas estatísticas importantes, sendo uma das principais o Teste de Hipótese.
O que é um Teste de Hipótese
Em síntese, um Teste de Hipótese envolve a formulação de duas hipóteses excludentes, ou seja, que não podem ser verdadeiras ao mesmo tempo. A primeira delas é chamada de Hipótese Nula (H₀), enquanto a outra é a Hipótese Alternativa (H₁).
A partir dos dados coletados, calcula-se uma estatística de teste, que está associada a uma determinada distribuição de probabilidade. Supondo que H₀ seja verdadeira, calculamos a probabilidade de observar os dados obtidos ou algo ainda mais extremo. Essa probabilidade é chamada de p-valor.
Geralmente, estabelece-se um ponto de corte para o p-valor, normalmente 5% (ou 0,05), para decidir se H₀ deve ser rejeitada. Assim:
- Se o valor-p for menor que 0,05, há evidências para rejeitar H₀ em favor de H₁.
- Caso contrário, não há evidências suficientes para rejeitar H₀.
É importante ressaltar que não se deve afirmar que se aceita H₀ ou H₁, pois o teste não garante esse tipo de conclusão com certeza.
Além disso, existem diversos tipos de Testes de Hipótese, e é essencial entender bem o problema e os dados para escolher a abordagem mais adequada. A aplicação incorreta de um teste pode gerar conclusões equivocadas, comprometendo a validade da pesquisa.
A seguir, veremos dois cenários práticos em que a aplicação de um Teste de Hipótese é fundamental. Para ambos os casos, utilizaremos como ponto de corte 0,05.
Exemplo 1 – Avaliando a eficácia de uma vacina
Neste primeiro exemplo, diante do surgimento de uma nova doença, foi realizado um experimento para avaliar a eficácia de uma vacina. Para isso, 100 pessoas, submetidas às mesmas condições, foram expostas ao agente causador da doença. Destas, 50 foram aleatoriamente selecionadas para receber a vacina.
Após o experimento, foi analisado quantos voluntários apresentaram sintomas, conforme mostrado na tabela abaixo:
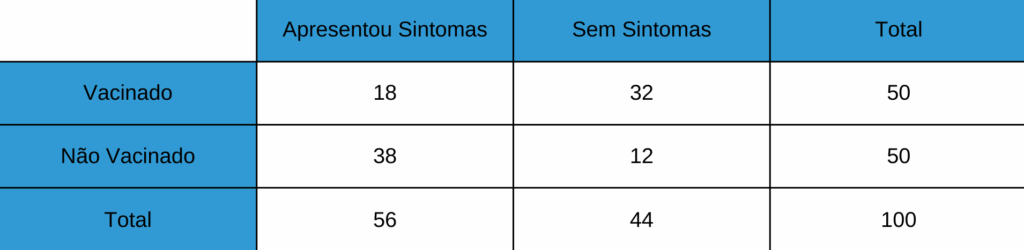
Para avaliar se a vacina é eficaz na prevenção da doença, é possível utilizar o Teste Exato de Fisher, que possui como hipóteses:
- H₀: As proporções de pessoas com sintomas são iguais nos dois grupos.
- H₁: As proporções de pessoas com sintomas são diferentes entre os grupos.
Com isso, aplicando o Teste Exato de Fisher, obtemos um p-valor de aproximadamente 0,0001, logo, há evidências para rejeitar a hipótese de que a proporção de pessoas com sintomas é diferente caso a pessoa tome ou não a vacina.
Exemplo 2 – Comparação das notas de duas turmas
Neste segundo exemplo, um professor deseja testar duas metodologias de ensino e verificar se há diferença nas médias das notas das turmas. Para isso, ele sorteou seus 300 alunos, distribuindo 150 para a turma A e 150 para a turma B. Cada turma foi submetida a uma metodologia diferente, e, após um mês de aulas, os alunos realizaram a mesma prova, que valia de 0 a 100 pontos.
A média da turma A foi 49, e a da turma B foi 53,4. As distribuições das notas podem ser visualizadas nos gráficos abaixo:
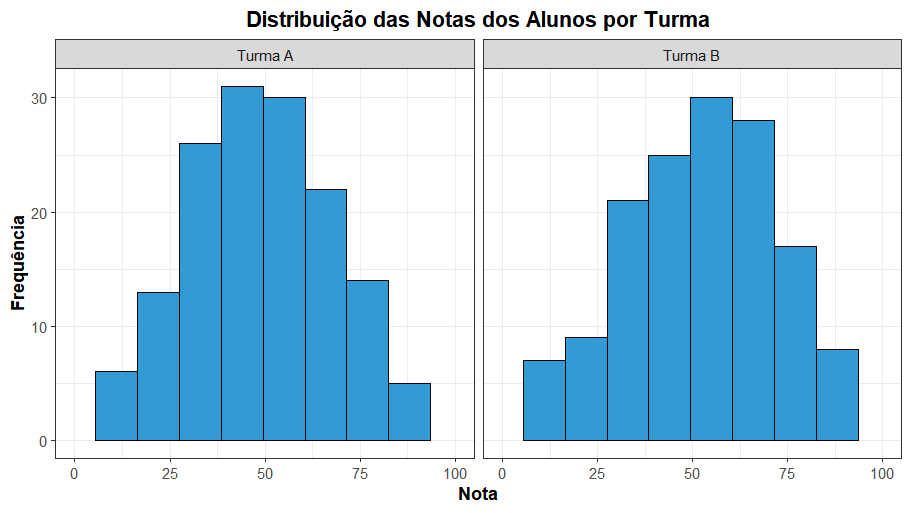
Para comparar a diferença entre as médias das duas turmas, neste caso podemos utilizar o Teste T, uma vez que suas suposições foram verificadas, e as hipóteses são dadas por:
- H₀: As médias das notas são iguais nas duas turmas.
- H₁: As médias das notas são diferentes entre as turmas.
Com isso, aplicando o Teste T, o p-valor obtido foi de 0,06355, logo, não há evidências para rejeitar a hipótese de que as médias das turmas são diferentes, ou seja, não há uma significância estatística para dizer que a metodologia de ensino altera a nota média dos alunos na prova.
Conclusão
Portanto, a Validação Estatística é uma etapa essencial para uma Pesquisa Científica, sendo diretamente responsável por garantir uma confiabilidade em resultados obtidos por meio de uma significância estatística.
Está ou estará trabalhando com alguma pesquisa? Entre em contato com a Estat Júnior, estamos prontos para garantir que os seus resultados obtidos tenham credibilidade utilizando inúmeros Testes de Hipótese.

